Beware Wolfram Alpha introductory offer!

So last year I signed up to Wolfram Alpha Pro with with an introductory offer of 3 months extra free.
That was on 30 April 2015.
Renewal date was set at 30 July 2016. All's good, that includes my 3 free months.

This year my subscription is renewed with the annual fee of $65.88 on 30 July 2016. OK, that is including the 3 months free.
However, the next renewal date is 30 April 2017!
That is 9 months for a 1 year subscription fee!!

So last year they gave me 3 months and this year they take the 3 months back!

That is NOT 3 months free, is it!

Shame on you Wolfram Alpha!

Proposed Scientific RPN HP Quickcalc

Inspired by Eddie's challenge, I created this:

It has all the functions of the original 1972 HP-35 and a few more. What more do you need for a handy scientific by-the-side-of-your-desktop calculator?

HP Prime : Funny Complex Trig in CAS View

(Update: this has been corrected in emulator version 5447 dated 2013-11-25)

OK, so posted some Prime results on the following forum:
For those that have an actual Prime calculator....

This refers to the emulator with firmware rev. 5106. From the link above it is evident that the first release of the actual Prime will give the same result.

Here's the screen capture again:

So what's my problem with this?

OK, apart from the "+-" and "--", quite a bit.

First, let's look at ACOS(2):

The "radian mode" answer is correct:

 (http://mathworld.wolfram.com/InverseTrigonometricFunctions.html equation 14)

This agrees with the symbolic radian mode answer of the Prime.

Numerically:

Now:

So:

But now let's look at the "degrees mode" answer. In the complex domain it is more common to continue with radian angles even when settings are in degrees. However, it is possible to do it in degrees, but it must be done carefully and correctly.

Let's look at the HP Prime approach:

Oh, oh, we are now subtracting a radian angle from degrees!!!

And that's how the Prime gets it's incorrect answer!!

The right way:





Similarly the Prime gets the wrong answer for ACOS(-2) in degrees mode.

Adding a crystal and capacitors the the HP-20b, HP-30b or WP-34s

Here is my experience of mounting the capacitors and crystal in the HP-30b or WP-34s.

The tools I used were simple:

Choosing the crystal and capacitor:
 Pretty much any 32.768 kHz crystal of the right dimensions will do. Usually you will find them under "watch crystals". I used the Abracon AB26T: http://www.abracon.com/Resonators/AB26T.pdf

Choosing the capacitors:
For information on attaching a crystal and capacitors to the AT91SAM7L processor used in the HP-20b/30b see this application note page 9:
http://www.atmel.com/Images/doc6369.pdf

Equivalent circuit:

Total capacitative load on the crystal is the 2 external capacitors in series (as far as the crystal is concerned, the ground connects C1 & C2 in series to itself) + the capacitance of the processor and stray capacitance in parallel:
CL = (C1*C2)/(C1+C2) + Ci  + Cs 

where:
CL = the capacitative load on the crystal
C1 & C2 are the 2 external capacitors we are going to add
Ci = internal capacitance of the processor for the crystal pins
Cs = stray (track & PCB) capacitance

If we keep the 2 external capacitors the same value: C1 = C2 = C
then
CL = C/2 + Ci + Cs

From the Atmel app note above: Ci = 2.5pF
From the crystal data sheet: CL = 12.5 pF
Cs estimated ~1 pF
thus C = (CL - (Ci + Cs))*2 = 18 pF

The Atmel datasheet specifies a maximum of 20pF, so 18pF is in the ball-park.

http://www.atmel.com/Images/Atmel_6257_32-bit-ARM7TDMI-Microcontroller_SAM7L_Datasheet.pdf (section 35.4.3 table 35-15).

For choice of capacitor, I avoided Y5V in this application as they have a wide capacitance variation with temperature which will alter the frequency of the crystal - not what we want for a stable clock.

I would recommend X7R or NP0/C0G. I used Multicomp - MC0603N180J500CT - (MLCC, 18pF, 5%, 50V, C0G / NP0, 0603).

The size of the capacitor is 0603 (1.6 x 0.8 mm).  This is the size of a grain of sand. Order more than two as it is easy to loose them!

(Note 0603 is the imperial size SMT, in metric it would be 1608. Be careful to check when ordering!!)

OK, so now for the mounting. I did the capacitors first and the the crystal.
Here are a video I made mounting the first capacitor:
(Note, I am not a professional solderer, but a home hobbyist)

The final product:

I hope you have fun doing yours :-)

(I ordered my crystal and caps in bulk, so have about 100 spare sets. Anyone want some for postage only, see eml below. Each set  will have 1 crystal and 4 caps).

Entering a complex number in vector on the HP-50G

Entering complex numbers can be done as folows:

Rectangular:
standard form: x + yi
or
vector form: (x,y)

Polar:
can only be entered as vector form: (r,<ø)

The HP-50G can only accept real numbers in Vector Form:
E.g.

is not allowed.


 It has to be entered as:




Here is one method to convert and enter the number (other suggestions welcome):

(note: change to "complex" mode at 00:12 is Press-and-Hold LeftShift & press i  (on TOOL button)

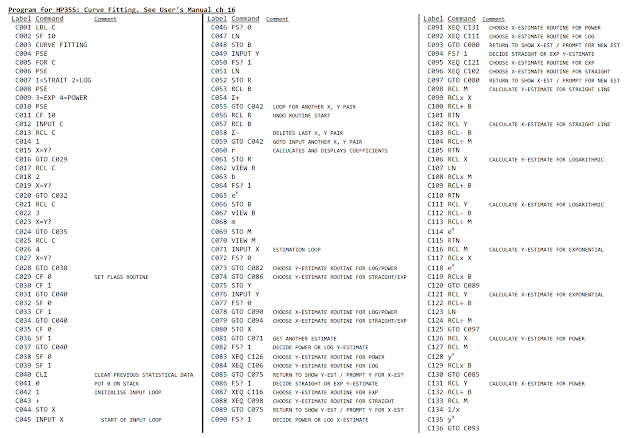
Curve fitting program for the HP-35s (combines the manual's programs into one label)

Chapter 16 of the HP-35s manual has programs for 4 different curve fittings. They are spread accross several labels and so take up valuable labels that could be used for other programs.

I have combined them into one label.

Here are instructions:

and here is the program listing:

Comments, suggestions & corrections welcome.

(Edit: updated as C065, C114 & C118 are e^x and C128 & C135 are y^x and were showing incorrectly)

Corrections in calculations on a modern "textbook" display calclator

Modern calculators that have a real textbook like display can offer advantages not only to inputting formulas, but when realising a mistake several steps down the line. Here is one such calculator that, when an error is corrected a few steps back, the updated results are automatically flowed down.

Here is the problem statement:

The respondent has come to the second part and written down some equations and decided to calculate it on the calculator. When the last answer seems a bit strange, an error is found in the earlier entry, corrected and the correct answer is immediately visible at the last calculation.